[Algorithm] 백준 2805

백준 2805

백준 2805, 이분 탐색(Binary Search)

문제

상근이는 나무 M미터가 필요하다. 근처에 나무를 구입할 곳이 모두 망해버렸기 때문에, 정부에 벌목 허가를 요청했다. 정부는 상근이네 집 근처의 나무 한 줄에 대한 벌목 허가를 내주었고, 상근이는 새로 구입한 목재절단기을 이용해서 나무를 구할것이다.

목재절단기는 다음과 같이 동작한다. 먼저, 상근이는 절단기에 높이 H를 지정해야 한다. 높이를 지정하면 톱날이 땅으로부터 H미터 위로 올라간다. 그 다음, 한 줄에 연속해있는 나무를 모두 절단해버린다. 따라서, 높이가 H보다 큰 나무는 H 위의 부분이 잘릴 것이고, 낮은 나무는 잘리지 않을 것이다. 예를 들어, 한 줄에 연속해있는 나무의 높이가 20, 15, 10, 17이라고 하자. 상근이가 높이를 15로 지정했다면, 나무를 자른 뒤의 높이는 15, 15, 10, 15가 될 것이고, 상근이는 길이가 5인 나무와 2인 나무를 들고 집에 갈 것이다. (총 7미터를 집에 들고 간다)

상근이는 환경에 매우 관심이 많기 때문에, 나무를 필요한 만큼만 집으로 가져가려고 한다. 이때, 적어도 M미터의 나무를 집에 가져가기 위해서 절단기에 설정할 수 있는 높이의 최댓값을 구하는 프로그램을 작성하시오.

입력

첫째 줄에 나무의 수 N과 상근이가 집으로 가져가려고 하는 나무의 길이 M이 주어진다. (1 ≤ N ≤ 1,000,000, 1 ≤ M ≤ 2,000,000,000)

둘째 줄에는 나무의 높이가 주어진다. 나무의 높이의 합은 항상 M을 넘기 때문에, 상근이는 집에 필요한 나무를 항상 가져갈 수 있다. 높이는 1,000,000,000보다 작거나 같은 양의 정수 또는 0이다.

출력

적어도 M미터의 나무를 집에 가져가기 위해서 절단기에 설정할 수 있는 높이의 최댓값을 출력한다.

접근 & 풀이

이미 이분 탐색이라는 것을 알고 접근했기 때문에 풀이 과정 자체는 쉬웠다.

하지만 이분 탐색이라는 것을 모르고 문제를 접했다면 이분 탐색으로

풀이를 한다는 접근을 어떻게 했을까

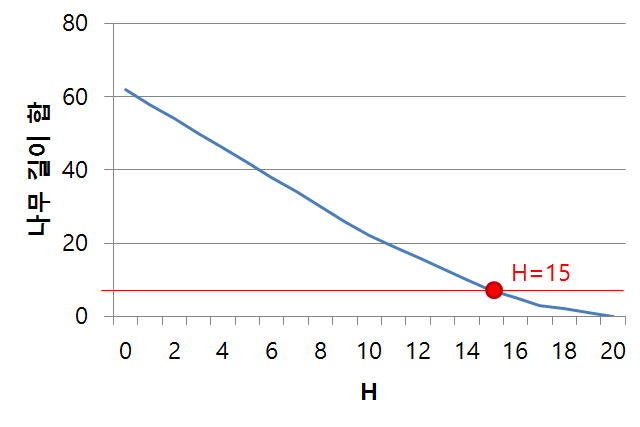
정답이 K라 할 때, H가 K보다 크면 나무를 잘라서 M미터 이상을 가져갈 수 없고, H가 K 이하면 M미터 이상을 가져갈 수 있습니다.

[출처] 이분 탐색(Binary Search) (수정 2019-02-15)|작성자 라이

시뮬레이션을 했을 때 H 가 커짐에 따라 가져가는 나무 길이의 합도 줄어든다.

반대로 작아지면 합이 커진다.

이를 통해 이분 탐색을 이용한다는 실마리를 잡을 수 있는것 같다.

코드

 import java.io.BufferedReader;
 import java.io.IOException;
 import java.io.InputStreamReader;
 ​
 public class B2805_e {
 ​
     public static void main(String[] args) throws IOException {
         BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
 ​
         String line = br.readLine();
         int N = Integer.parseInt(line.split("\\s+")[0]),
                 M = Integer.parseInt(line.split("\\s+")[1]);
 ​
         line = br.readLine();
         String[] strH = line.split("\\s+");
         int[] H = new int[N];
         for (int i=0; i<H.length; i++) {
             H[i] = Integer.parseInt(strH[i]);
         }
 ​
         int lo = 0, hi = 1000000000;
         while(lo +1 < hi) {
             int mid = (lo+hi)/2;
 ​
             long sum = 0;
             for (int i=0; i<N; i++) {
                 if (H[i] > mid) {
                     sum += H[i] - mid;
                 }
             }
 ​
             if (sum >= M)
                 lo = mid;
             else
                 hi = mid;
         }
 ​
         System.out.println(lo);
         br.close();
     }
 ​
 }